HackerRank Kangaroo Solution

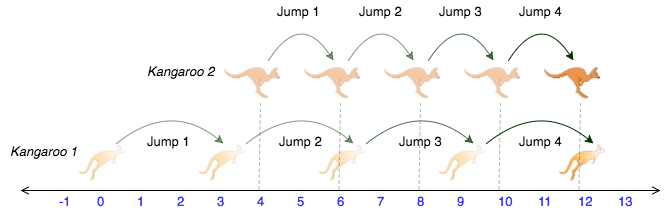
You are choreographing a circus show with various animals. For one act, you are given two kangaroos on a number line ready to jump in the positive direction (i.e, toward positive infinity).

– The first kangaroo starts at location and moves at a rate of meters per jump.
– The second kangaroo starts at location and moves at a rate of meters per jump.

You have to figure out a way to get both kangaroos at the same location at the same time as part of the show. If it is possible, return YES, otherwise return NO.

For example: kangaroo starts at x1 = 2 with a velocity of v1 = 1 and kangaroo 2 starts at x2 = 1 with a velocity of v2 = 2; after one jump, they are both at x = 3 (x+1 + v1 = 2+1, x2 + v2 = 1+2), so the answer is YES.

Function description:

Complete the function kangaroo in the editor below. It should return YES if they reach the same position at the same time, or NOif they don’t.

The kangaroos have the following parameter(s):

– x1, v1: Integers, starting position and jump distance for kangaroo 1
– x2, v2: Integers, starting position and jump distance for kangaroo 2

Constraints:
– 0 < x1 < x2 < 10000
– 1 < v1 < 10000
– 1 < v2 < 10000

Solution

So my first thought was that, according to the constraints, the max limit wasn’t a huge number (10,000), so I thouhgt that it would be easy to get to the answer if I just loop until x1 + v1 * i == x2 + v2 * i, or 10000 was hit. But, then I realized that like anything in our software world, constraints are never respected, so eventually, I would find myself adding zeros to the limit.

So, the most efficient way was to create an equation of the problem to get to the solution, and it was easy.

If we were to describe the problem as en equation, we would need to write that:

x1 (kangaroo 1 initial positon) plus n jumps times v1 kangarooo 1 velocity) equals x2 (kangaroo 2 initial positon) plus n jumps times v2 kangarooo 2 velocity):

(x1 + n*v1) = (x2 + n*v2)

And from there, we just need to solve the equation:

n * v1 – n* v2 = x2 – x1
n * (v1 – v2) = x2 – x2
n = (x2 – x1) / (v1 – v2)

We now know the formula to check the number of jumps needed (n), and, we can say that if n is not an integer, then the kangaroos will never meet.

So we can write a little code. In my case, I chose Python as the language to solve the problem:

return "YES" if (x2 - x1) % (v1 - v2) == 0 else "NO"

But, what happened if the kangaroos have the save velocity? We would be facing a black hole because we would be dividing by zero, so we need to ensure that we don’t destroy the universe:

if v1 == v2:
    return "NO"
return "YES" if (x2 - x1) % (v1 - v2) == 0 else "NO"

Also, I realized that there would be obvious cases where the kangaroos would never meet, so we can address them even before bothering doing the math. For example, if one kangaroo had a position ahead and its velocity was also faster, then they would never meet, so we can discard this scenario:

 if x1 > x2 and v1 > v2:
    return "NO"
 if x1 < x2 and v1 < v2:
    return "NO"
 if v1 == v2:
    return "NO"
    
return "YES" if (x2 - x1) % (v1 - v2) == 0 else "NO"

Now, we have a very efficient solution that passes all the test cases.